研究領域.數學建模與科學計算
快速連結
一、數學建模與科學計算簡介
科學計算是現今最具整合型的研發領域之一。由於電腦軟體與硬體的高度與快速發展,科學計算已成為物理、化學、電子、機械、土木、生物、醫學、經濟等多種領域不可或缺的研究工具。計算方法已與理論方法、實驗方法鼎足而立,成為人類解決問題的重要工具。
人類藉由電腦幫助研究,探討科學問題的主要過程是:觀察現象與實驗→數學模型化→數值模擬→與實驗相佐證→解決問題。圖一說明了一個典型的科學計算流程以及科學計算如何扮演整合角色。
很多實際問題,如天氣預測,能源消耗,飛機與汽車的安全設計,生物醫學的心臟模擬,奈米材料的研發,衍生性金融產品的定價,甚至飛彈的模擬試射等等,透過物理學家或相關領域學者的觀察與實驗,這些問題,往往可以被一組代數或常(偏) 微分方程式來描述,這種過程,便是將實際問題數學模型化。這種模型化的適切性與否,必須藉由數學分析與數值模擬和實驗數據相佐證。當前,數學建模與科學計算相結合的研究方法,提供比傳統實驗科學更具安全與經濟。尤其在不易做實驗的生命科學,更顯得重要性。
軟體產業是邁入21世紀我國所擬定提昇全球競爭力的策略性產業之一,1999年10月「南港軟體工業園區」之開幕使用,象徵台灣進入軟體高科技領域的新紀元。1820年代英國數學家Augusta Ada Byron是人類第一位電腦程式設計師,全球資深的軟體工程師皆知,嚴謹、抽象、去蕪存菁的大學數學教育是開發軟體最佳的基礎養成教育之一,數學系畢業生具軟體工程基本知識,將是未來職場最熱門的高科技生力軍之一。
Top
數學是科學計算的核心,也是描述各種不同科學與工程問題最具一般性與嚴謹性的語言。軟體工程是結合數學與應用科學的主要工具,本領域的研發重點大概分為:
- 數學模型化(Mathematical Modeling):
正如圖一所示,正確而有用的數學模型是由觀察、實驗、與模擬反覆進行得來的,也是科學計算過程中最關鍵的部份,依數學本質而言模型化的類型又可約略分為:
- 常微分方程(Ordinary Differential Equations)
- 偏微分方程(Partial Differential Equations)
- 線性與非線性代數(Linear and Nonlinear Equations)
- 數值方法(Numerical Methods):
數值方法研究的基本精神是提供人們一個方便、快速、節省、且可信的計算環境,計算方法的突破可造成科學、工程發展的突飛猛進,這種例子屢見不鮮,如快速富氏變換、多重網格法、平行與分散式計算法、適應性計算法等。
 |
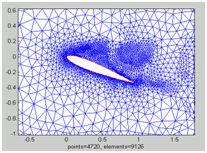 |
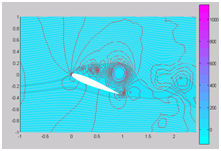
| The above figures show the simulation of high Reynolds number incompressible flow passing an airfoil. Our solver consists of the SUPG finite element discretization on vortices adapted mesh and multigrid preconditioned linear solver. | |
 |
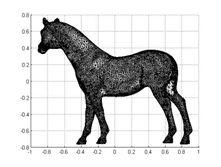 |
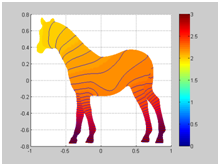
| The above figures show heat diffusion on the horse surface and the computation meshes downloaded from internet. Our surface finite element solver is based on the evolution surface finite element method proposed by Dziuk and Elliott, 2007. | |
 |
|
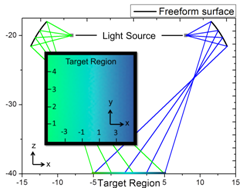
| The above figure shows an optical system computed from our free-form generator. The system is designed to create a wall shower with linear color change. The Monge-Ampere type of PDE for the free-form reconstruction is approximated using Hermit finite element |
Top
二、老師的研究興趣
林文偉 教授(數值分析、矩陣理論及計算、最優化控制、計算共形幾何)
|
本實驗室為「計算共形幾何與數值計算研究室」隸屬於交大應數系丘成桐中心, |
|
本實驗室研究主要包含以下兩部分: (a) 三維馬克斯威爾方程的特徵分解和快速特徵值演算法: | 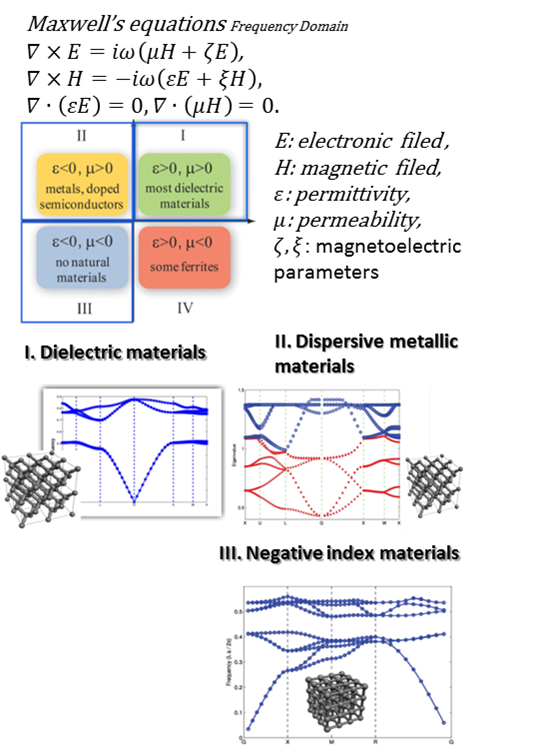 |
|
(b) 三維計算共形幾何以及其應用: |
 |
賴明治 教授(偏微分方程數值算法、複雜流體系統之數值模擬)
|
在應用數學的世界裡,界面流之研究一直是人們主要關心的議題,並在許多自然界現象或是工業應用中扮演重要的角色,特別是在軟物質以及微流體系統。我們已成功地應用沉浸邊界法 (immersed boundary method) 發展出數種簡單且有效率的數值方法來模擬帶有界面活性劑之流體系統問題以及囊泡 (vesicle) 流體動態系統,其簡述如下: 一.帶有可溶/不可溶之界面活性劑的界面流問題: 二.囊泡流體動態系統: |
 |
石至文 教授(動態系統、微分方程、生物數學)
|
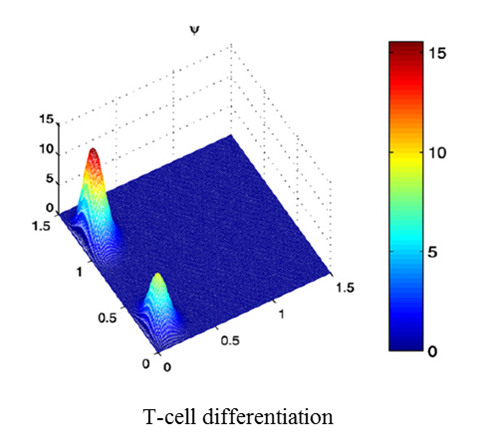
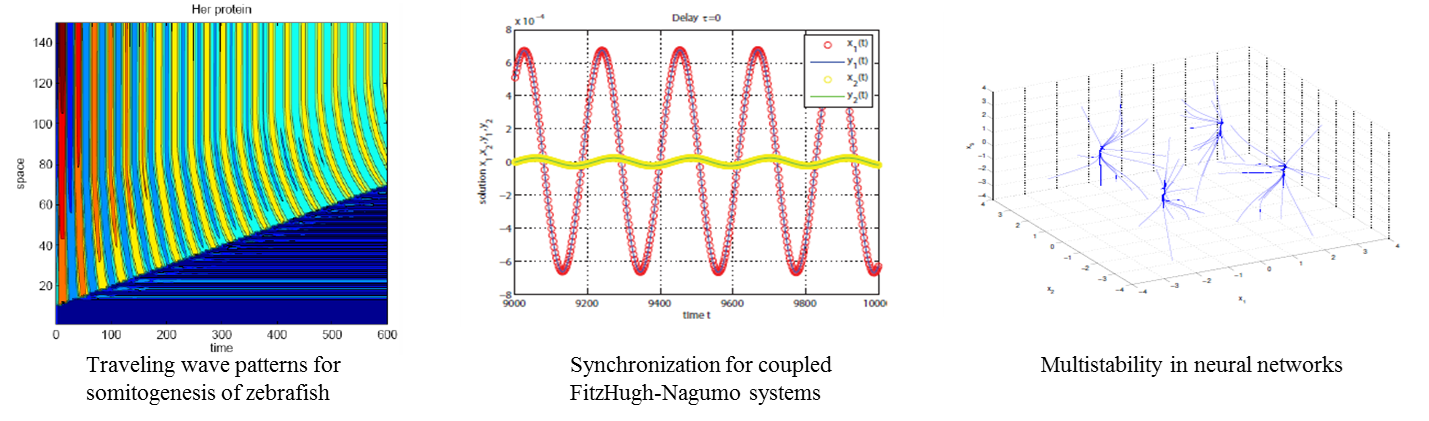
研究興趣主要是發展數學方法,研究非線性系統的動態性質;並將動態學理論應用在一些生物現象或生物問題的數學模型分析;包含細胞分化(cell differentiation)、骨節生成(somitogenesis)、基因調控(gene regulation)、神經系統(neuron system)、生態系統(ecological system),而對這些數學模型方程式有較完整的了解。另一研究興趣為有關類神經網路 (neural networks) 之數學理論。各種類神經網路之數學模式一般可以描述為連續時間或離散時間之微分方程。 |
 |
 |
莊 重 教授(耦合系統、同步化、神經網路、神經元動態、群聚問題、車流模型)
|
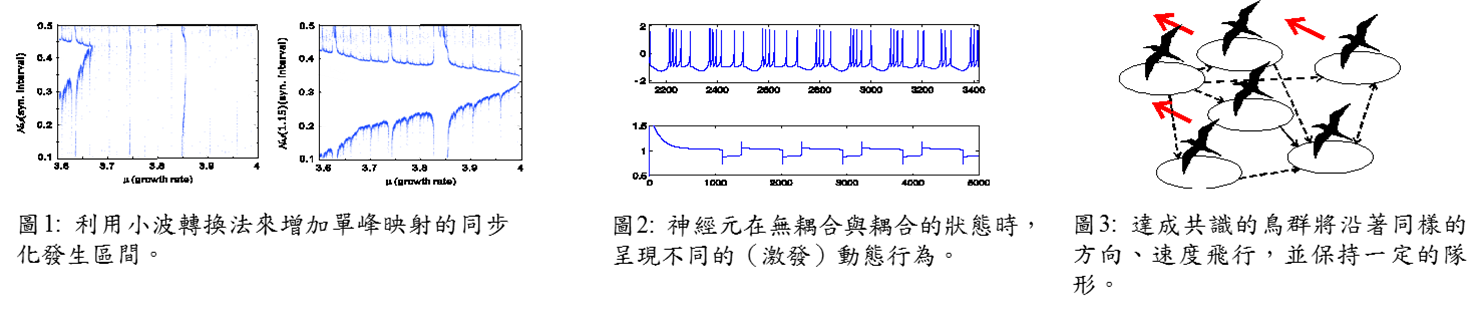
我們的研究興趣主要在於能被模型成耦合網路模型的真實世界問題。這些考慮的問題包含了以下所列:(i)耦合混沌振盪器; 耦合映射網格:在過去的幾年裡,我們研究許多在耦合網路中的同步化現象,並且做出一些分析的理論結果來闡述同步化發生可能性。這些結果能被應用在實際電路系統的設計以及通訊加密上(見圖一)。 (ii) 神經網路; 神經傳導路徑:近幾年來在研究神經元的(激發)動態行為研究,研究的興趣已由研究單一個神經元延伸到整個神經元網路。而我們所關注的是在研究神經元在神經網路的同步現象,以及探討在不同程度的連結耦合下,神經細胞將呈現何種不同的動態行為 (見圖二)。 (iii) 群聚行為, 存在於生物群體間,諸如鳥、魚、細菌、昆蟲,的共同行為: 最近,我們也考慮了生物體的群聚現象並且討論生物於群聚中會避免碰撞的機制(見圖三) 。 (iv)傳染病模型; 疾病傳染模型: 我們的團隊對於研究人與人之間的接觸網路、人們對疫情認知的程度與感染媒介對於疾病的散播影響也有興趣。 (v)微觀和巨觀的車流模型: 交通堵塞問題亦是我們有興趣研究的項目之一。我們利用一些車流模型來解釋車流與交通堵塞的發生。將來,我們企圖用車流模型來解釋台灣高速公路的車流情形。 |
 |
葉立明 教授(數值分析、微分方程)
|
我最近的研究主題是探討流體在不均勻介質中的傳輸與擴散問題。這問題是由描述地底下污染源的傳輸,二相介質中的熱傳導,合成物質的張力問題等得到。我主要是考慮這些問題的數學模式的推導,解的收斂性質,及解的數值計算。 考慮一個定義在有週期性質的定義域(週期為ε)上的橢圓方程式。當ε趨近於0時,我們知道方程式的解會收斂到某一個簡單的方程式的解,收斂的速度也可估算出來。對實際的現象我們也想問同樣的問題。假設我們有一個描述實際現象的數學方程式時,(1)我們是否可證明此方程式的解,在很長的時間後與在很大的範圍下,會收歛到某一個簡單方程式的解? (2)若會收斂,則收斂速度為何? (3)是否有一簡單的數值方法可計算描述實際現象的數學方程式的解? 想要回答以上的問題,有幾個基本數學工具是必需的,例如偏微分方程式,遍歷性理論,各種函數空間,均質化方法,及數值計算方法。 |
吳金典 副教授(數值偏微分方程、有限元素法、多重網格、三維影像)
|
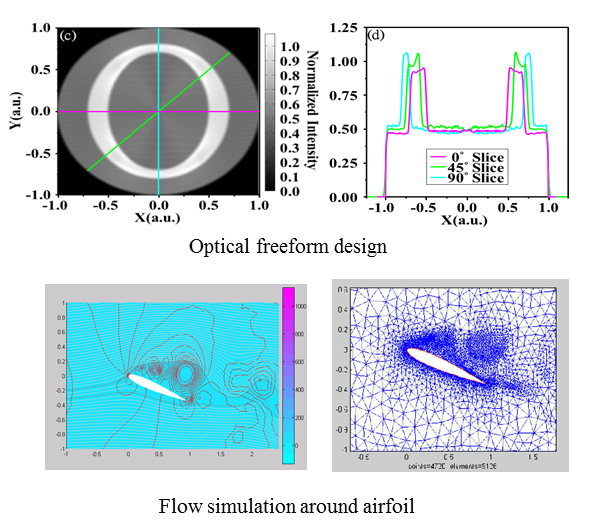
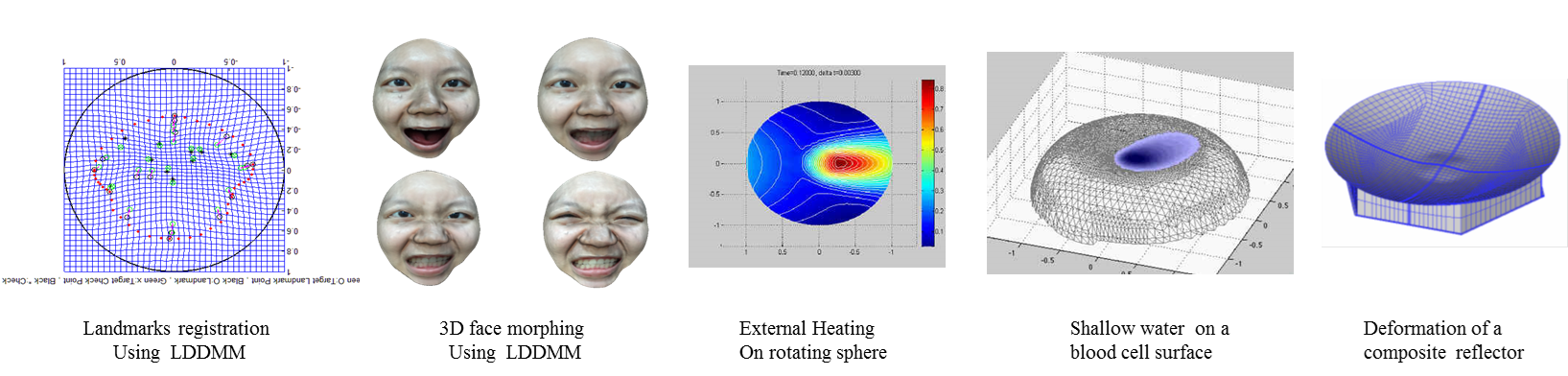
我的研究興趣在科學計算的理論與應用。特別是利用有限元素法(FEM)來計算許多來自工程方面的問題,包括流體力學,彈性力學,與幾何光學等。流體力學方面,我們對不可壓縮流的 Navier-Stoke方程,淺流的Shallow water方程與薄膜,潤滑的 thinfilm方程的數值計算有興趣,彈性力學方面,我們對幾何非線性薄膜,碳纖合成板殼以及壓電材料的型變有興趣,並將部分的研究成果應用在三維影像中的幾何形變的處理,而幾何光學的部分,我們運用Monge-Ampere的高階有限元素的數值解來設計光學鏡面。在計算的效能部分,我們則利用多重網格法搭配Krylov space來加速。 至於三維影像的部分,包含三維建模,影像追蹤,機器學習等,目前也是我們主要的研究方向。 |
 |
 |
張書銘 副教授(科學計算、動態系統)
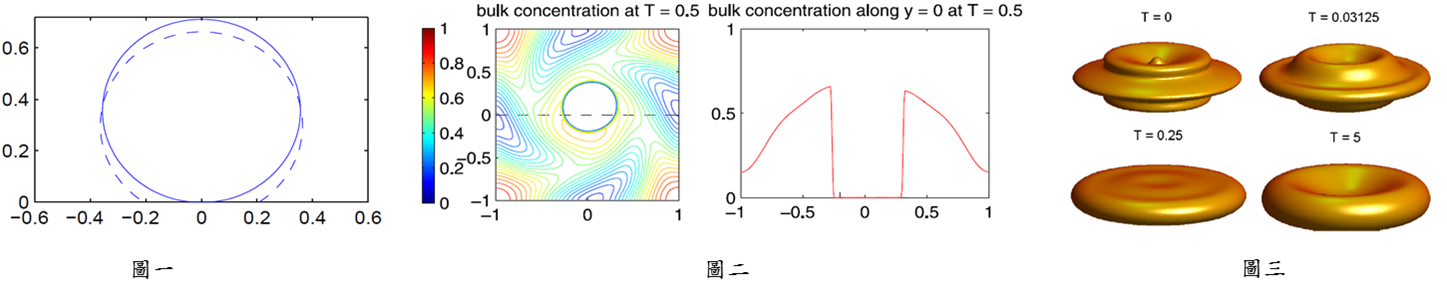
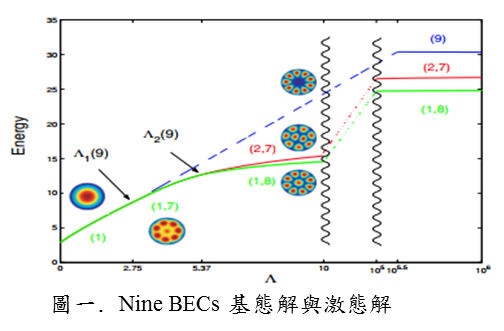
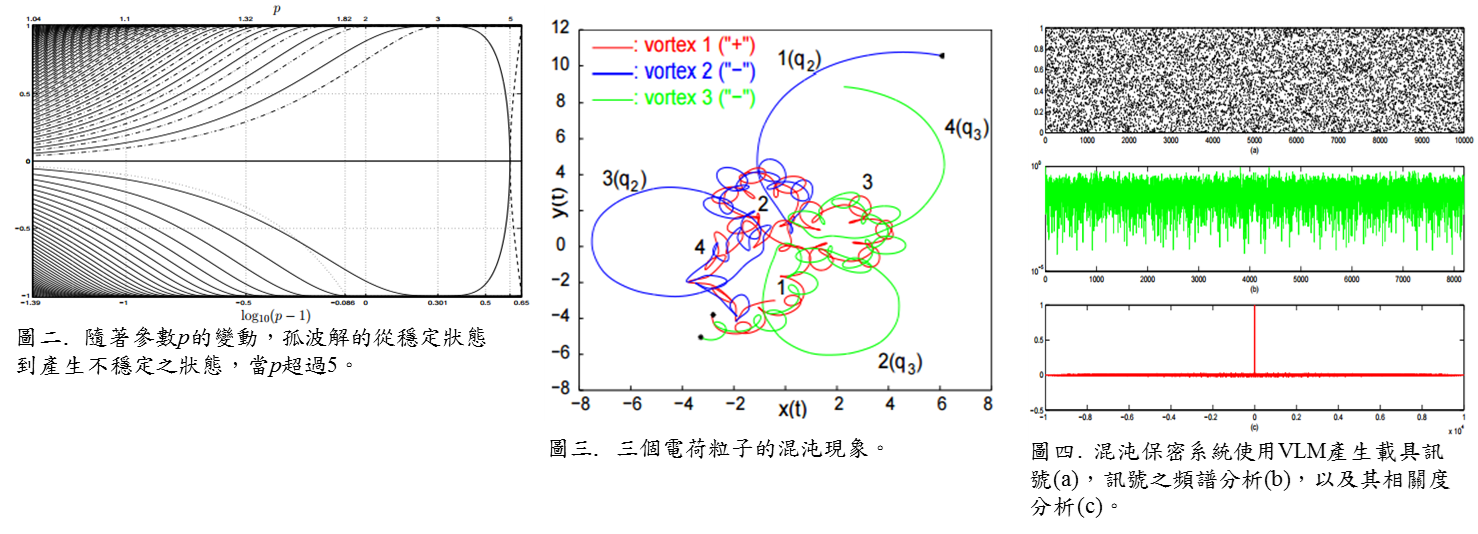
在科學計算此研究領域的研究趣向是在「非線性薛丁格方程之數值計算」上,探討(I)求解玻色愛因斯坦凝聚(BEC)現象之基態解與激態解(圖一) &(II)孤波解的穩定分析(圖二)。另外,在動態系統此研究領域的研究趣向是在「動態系統之混沌現象與其應用」上,探討(III)混沌現象之發掘(圖三) &(IV)混沌現象應用於保密通訊(圖四)。 |
 |
 |
陳子軒 副教授(粘性不可壓縮流體流動偏微分方程分析、幾何和拓撲性質)
|
黏性不可壓流體之解析、幾何、及拓樸性質,偏微分方程眾所周知,不可壓的黏性流體之動態乃由不可壓的維納-斯托克斯方程所描述,雖然在十九世紀科學界已熟知如何由牛頓第二定理導出維納-斯托克斯方程,但要遲至1930年代至1950年代之間,當Leray以及Hopf建立起一套維納-斯托克斯方程之弱解之存在性理論時,真正現代意義的,以偏微分方程為立足點的數理流體力學才算真正伊始。 自此之後,在這領域的專家們開始致力於建立Leray-Hopf弱解之光滑性,特別是在弱解帶有某種 “時─空”可積條件之下,但至今為止,是否可能出現弱解在有限時域內爆破而導致光滑性之喪失仍是為解決之大問題。 我們的研究致力於探討發生於非平坦背景空間之不可壓黏性流體之解析、幾何以及拓樸性質,在近年,吾與Magdalena Czubak教授率先觀察在一負曲率曲面之有限能量不可壓黏性流體之非唯一性現象,隨之並建立起一套弱解理論以修補非依性所衍生之差謬。 在不久的將來,吾人欲建立非平坦空間之流體理論與經典平坦空間流體理論間之關聯。 |
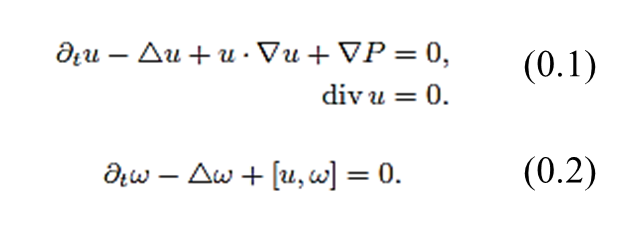 |
林得勝 副教授(數學建模、科學計算、流體力學、漸進分析)
|
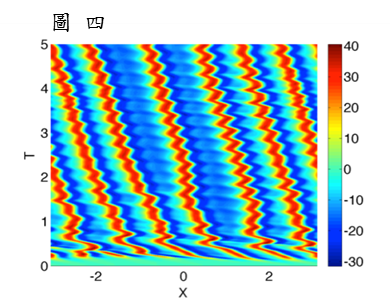
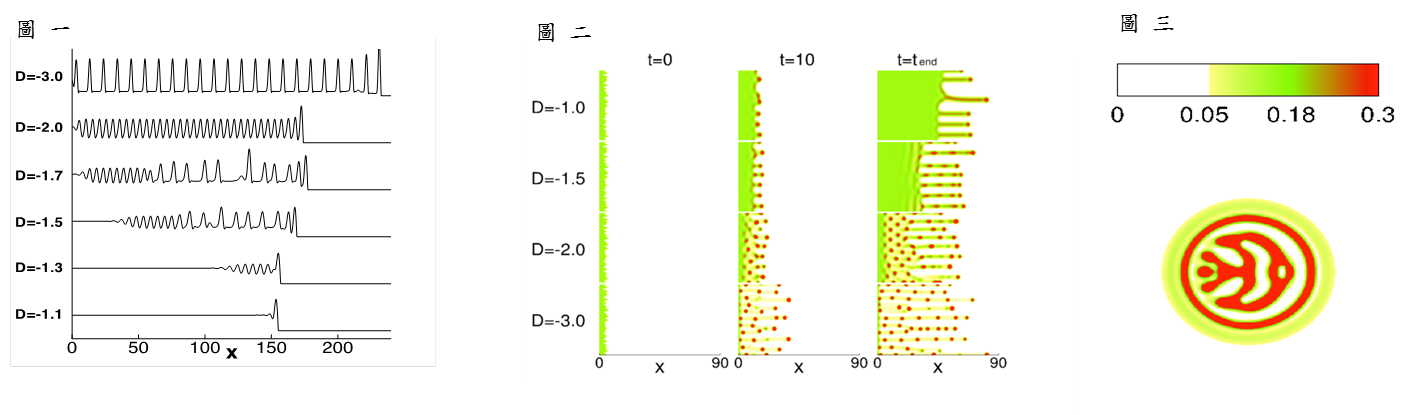
我的研究方向主要是發展分析及計算的數學工具,來解決並用於流體相關問題中所發展出來的數學模型。目前主要研究薄膜流體,此外,我也會與其他領域的科學家合作解決真實的工程問題。 我目前研究主題包含: (1) 牛頓薄膜流體中的手指狀不穩定性; (2) 向列型液晶薄膜的建模與分析; (3)非局部色散-主動耗散系統中的相干結構; (4) 電化降膜流中孤立脈波的互動以及束縛態理論。 舉例來說, 圖一及圖二分別為二維及三維的計算模擬降膜流中的手指狀不穩定性。 圖三則是向列型液晶薄膜其表面的花漾生成模擬。 圖四則是模擬薄膜流體被紊流氣體所推動時其表現孤立脈波的互動情形。 |
 |
 |
薛名成 副教授(數值分析、科學計算、地球流體力學)
|
目前研究興趣,主要著重偏微分方程式的計算和分析。偏微分方程式的主要來自地球流體地學的物理模式。其中,感興趣的物理模式包括Primitive equations 和Shallow water equations等等。這些方程式是用來描述在海洋或大氣流體運動行為或為天氣預測的基本方程式。 圖表一,主要是呈現在地球流體力學中,各種尺度下物理相關模式的示意圖。Navier-Stokes 方程式是最基本描述流體運動的方程式。由於三維度方程式本身相當複雜且困難,因此,藉由地球上海洋或大氣的thin layer 結構 (也就物理垂直空間尺度相對於水平尺度的比值小),學者簡化原本複雜Navier-Stokes equations ,得到Primitive equations。如果只考慮Primitive equations 的first mode (也就是方程式的垂直平均訊息),則得到Shallow water equations。 |
 |
|
目前研究主要課題如下: 詳細資料,請參考我的網頁(QR code) (圖二)。 |
余啟哲 助理教授(微分方程、科學計算)
Top
三、相關選修課程
- 微分方程(大二)
- 數值分析(大三、研究所)
- 科學計算(大三、大四、研究所)
- 半導體數學與軟體工程(大三、大四、研究所)
- 矩陣計算(大三、大四、研究所)
- 數值偏微分方程(大三、大四、研究所)
- 實變函數論(大三、大四、研究所)
- 泛函分析(研究所)
- 應用泛函分析(研究所)
- 偏微分方程(大二、研究所)
- 應用數學方法(研究所)
- 有限元素法(研究所)
Top