研究領域．微分方程與動態系統
快速連結
一、「微分方程與動態系統」簡介
動態系統為自然界各種物理系統、生態系統、工程系統隨時間演化之描述。這些系統通常是以微分方程來表現，包含常微分方程(ordinary differential equations)，偏微分方程(partial differential equations)，泛函微分方程(functional differential equations)等。另有離散時間(discrete time)之動態系統與新近發展之網格型動態系統(lattice dynamical system)等。
動態系統現今已成為一跨領域(interdisciplinary)的科學，其起源可追自十七世紀中期，牛頓描述基本運動定律與喀普勒(Kepler's)行星運轉定律之時。所以動態系統與微分方成源自物理。至今其與物理的關連性仍然相當密切。舉例來說，美國太空總署在2001年有一收集太陽塵之飛行任務─Genesis Discovery Mission，集合了加州理工學院JPL實驗室與歐洲等地之數學家、天文物理學家來設計一特殊節省燃料之軌道，在這個工作中以古典力學為基礎，利用對n-體問題之瞭解，運用數學分析與電腦輔助計算來進行。
另一方面，在生態學、生物數學與電路理論之發展上，動態系統也扮演了很重要的角色。例如，1963年諾貝爾生理醫學獎得主Hodgkin and Huxley 之工作即為探討生物細胞之訊號傳遞，其所做之研究內容即為微分方程解之分析與計算及其在生物學現象之解釋。而電路理論之具體架構亦是利用微分方程來呈現。這幾年來，本系幾位老師在細胞型類神經網路的數學理論研究上頗有進展；在隱密訊號傳遞與同步化理論上亦展開積極的研究工作。
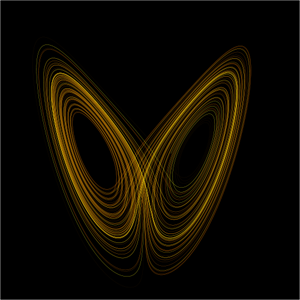
近年來之熱門話題，混沌現象(chaos)與碎形(fractals)與動態系統有密切關連。混沌為一自然現象，瞭解、掌握盡而利用此一現象，將是新世紀科技領域的重要進展。本系有幾位老師目前在混沌現象的數學分析與計算亦投入相當之努力；包含離散時間之動態系統、網格型系統混沌現象之數學描述，混沌形成之機制，及混沌之控制與同步化(synchronization)。所討論的方程式來自於電路理論、光電效應、生態模型、流體力學等。
Top二、老師的研究興趣
林松山 老師 (動態系統、Zeta函數)
|
本人研究領域為多維符號動態系統及動態Zeta函數。 1.多維符號動態系統： 2.動態Zeta函數： |
林文偉 老師 （數值分析、矩陣理論及計算、最優化控制、計算共形幾何）
Top石至文 老師 (動態系統、微分方程、生物數學)
Top李明佳 老師 (動態系統、混沌)
|
近年來，我們研究了以下幾個主題： (1) Henon函數族之不變集具有及不具有SRB測度的共存現像 (2)帶有覆蓋關係及Liapunov條件的函數擾動成多維度系統後的拓撲動態 (3)同宿拓撲交叉多維度擾動的正拓撲熵 (4)耦合映像網絡的覆蓋關係 (5)差分動態關係及其多維擾動系統之符號嵌入的穩定性。 |
莊 重 老師 （耦合系統、同步化、神經網路、神經元動態、群聚問題、車流模型）
Top
李榮耀 老師 （黎曼空間理論、古典數學函數理論、週期性孤立子方程理論及其應用於波動）
|
我們在N相的黎曼空間上發展完全可積之進展方程式的週期性孤立子理論， 並將其應用於廣泛的波動實務上。 我們有系統的用下列三步驟進行研究， 且理論分析與數值運算並行: (1) 在不同之代數結構下的黎曼空間上， 發展正確之複變函數理論及路徑積分的技巧， 這是研究波的最基本而重要的工具。 (2) 研習古典數學函數理論如 Elliptic 函數， the Theta 函數,及 the Jacobian Elliptic 函數， 它們提供了黎曼空間理論及波動理論非常重要的理論基礎。 (3) 把 (1, 2) 的理論與數值運算技巧來分析研究完全可積之進展方程式如 Korteweg-de Vries， sine-Gordon and nonlinear Schrdinger非線性偏微分方程系統。 這些方程式是廣泛被使用之重要波動問題的數學模式。 波動問題的研究還需要很多不同的數學理論及工具， 仍是待開發的領域。而週期性孤立子理論果已成功應用於各類水波(深、 淺、 長、 短)， 光波(如雷射)， 聲波， 訊號等。 |
張書銘 老師 （科學計算、動態系統）
在「動態系統」上，本人的研究趣向是在「動態系統之混沌現象與其應用」上，目前的研究成果可分為兩類，（I）混沌現象之發掘；（II）混沌現象應用於保密通訊。於混沌現象之發掘中，是關於混沌現象之發掘的工作，又有三種研究型態，一種是運用數學理論嚴格證明混沌現象的存在；另一種是藉由數值模擬的方式找尋並佐證混沌現象之存在，最後一種是在實驗室直接將混沌現象製造並呈現出來。於混沌現象應用於保密通訊中，是藉由混沌動態系統的混亂現象，實地的發展出一通訊系統架構，應用於保密通訊上。此保密通訊架構，不同於傳統的編碼，亦非屬最大質數加密法之保密理論。
Top余啟哲 老師（微分方程、科學計算）
Top三、相關選修課程
本系每年開設之動態系統與微分方程相關課程：
- 微分方程 (大二)，
- 動態系統簡介 (大三、四)，
- 常微分方程 (大四、研究所)，
- 偏微分方程 (大四、研究所)，
- 動態系統 (大四、研究所)，
- 混沌動態系統 (大四、研究所)， Top