Research Fields: Mathematical Modeling and Scientific Computing
Quick Links
- General Introduction to Mathematical Modeling and Scientific Computing.
- Faculty and Research Interests.
- Annual Courses.
- Graduates and Employment.
General Introduction to Mathematical Modeling and Scientific Computing
Scientific Computation is presently one of the most readily integrated research and development fields. Due to the rapid development of computer software and hardware, scientific computation has become the indispensable problem solving tool in physics, chemistry, electronics, mechanics, civil engineering, biology, medicine, economics, etc.. Computational, theoretical, and experimental methods are the foremost means of problem solving.
People utilize the power of computer in the investigation of scientific curiosities as follows: observation and experiment → mathematical modeling → numerical simulation → experiment data compliance → problem solving. Figure 1 explains a typical process and the integrated role of scientific computation.
Many real problems such as weather prediction, energy consumption, safety design for aircraft and automobile, artificial hearts in biomedicine, development of materials using nanotechnology, the pricing of derivative financial products, missile simulation etc. can be described by ordinary or partial differential equations. These processes are called mathematical modeling. However, the adaptivity of the mathematical modeling must depend on the compliance between mathematical analysis, numerical simulations and experimental data. Nowadays, solving real-life problems by combining mathematical modeling and scientific computing provides better safety and economic benefits compared to conventional experimental science. In particular, the approach appears more important when it is not easy to conduct experiments in biomedicine.
Entering the 21st century, software industry is included in the national strategic industries drafted to raise the nation's global competency. The opening of Nankang Software Park in October 1999 symbolized a new era for Taiwan high tech software industry. In the 1820s, Augusgta Ada Byron, an English mathematican, is the world's very first computer software designer. It is obvious to experienced software engineers that the rigorous and abstract college mathematics education is one of the most desirable background educations. Mathematics graduates equipped with fundamental software engineering ability are one of the most sought after recruits.
Mathematics is the soul of scientific computation and also a rigorous general language to describe various scientific and engineering problems. Software engineering is a major means to integrate mathematics and applied sciences. The major research orientations of this field are as follows:
- Mathematical Modeling:
- Ordinary Differential Equations
- Partial Differential Equations
- Linear and Nonlinear Equations
- Numerical Methods:
 |
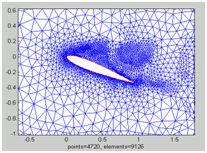 |
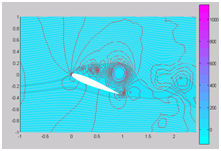
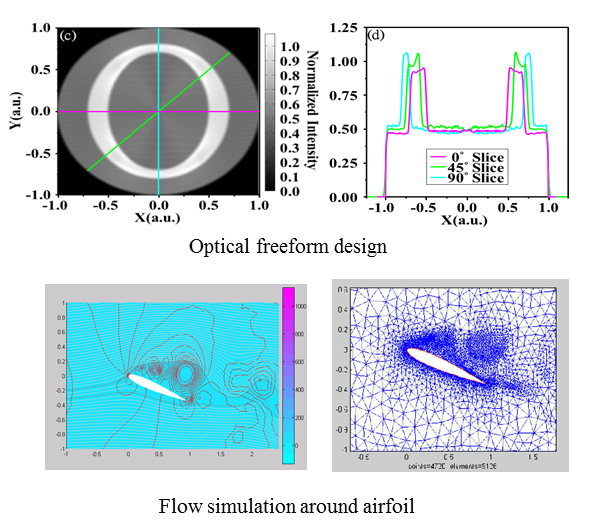
| The above figures show the simulation of high Reynolds number incompressible flow passing an airfoil. Our solver consists of the SUPG finite element discretization on vortices adapted mesh and multigrid preconditioned linear solver. | |
 |
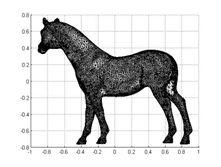 |
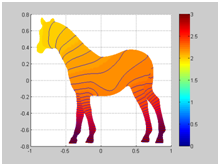
| The above figures show heat diffusion on the horse surface and the computation meshes downloaded from internet. Our surface finite element solver is based on the evolution surface finite element method proposed by Dziuk and Elliott, 2007. | |
 |
|
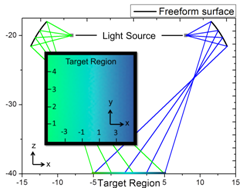
| The above figure shows an optical system computed from our free-form generator. The system is designed to create a wall shower with linear color change. The Monge-Ampere type of PDE for the free-form reconstruction is approximated using Hermit finite element |
Top
Faculty and Research Interests
Professor Lin, Wen-Wei (Numerical Analysis, Matrix Theory and Computation, Optimization, Computational Conformal Geometry)
|
We are a research group on “Numerical Algebra and Geometry” in the ST Yau Center and Applied Math Department , nycu. |
|
Our primary research interests include the following two parts: (a) Eigendecomposition and Fast Eigensolver for 3D Maxwell’s equations: | 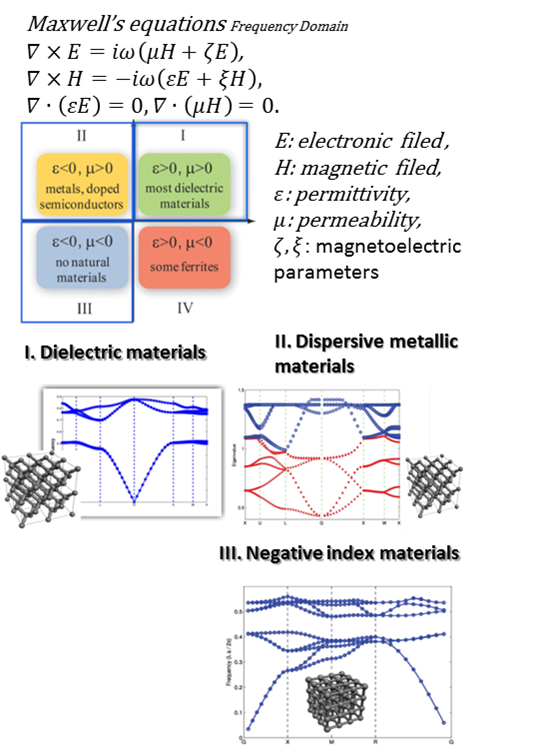 |
|
(b) 3D Computational conformal geometry with applications: |
 |
Professor Lai, Ming-Chih (Numerical methods for PDEs, Complex fluid dynamics simulations)
|
The study of the incompressible flows with interfaces is of major interests among applied mathematics community. It plays an important role in numerous natural phenomena and industrial applications, especially, for the soft matter physics and hydrodynamics of micro-fluidic systems. We have successfully developed simple and efficient numerical schemes based on immersed boundary method for simulating fluid-surfactant and fluid-vesicle dynamics. Brief descriptions are as follows: (I) Interfacial flows with insoluble/soluble surfactant: (II) Vesicle hydrodynamics: |
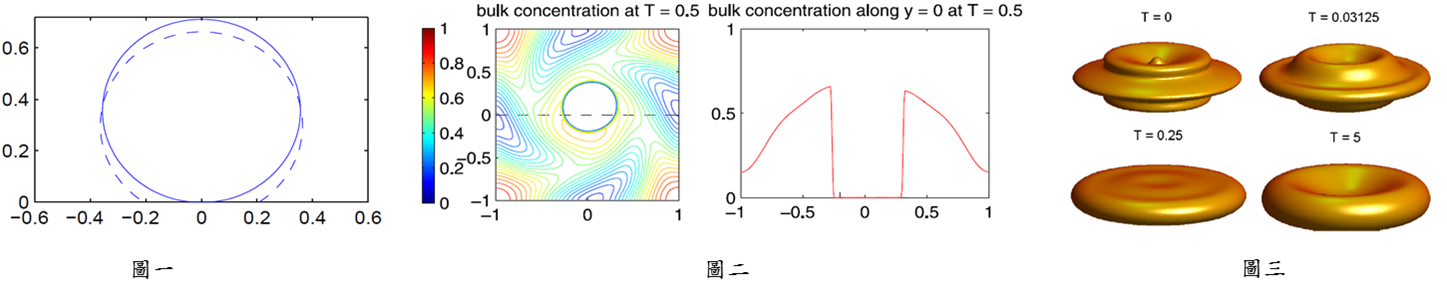 |
Professor Shih, Chih-Wen (Dynamical systems, Differential equations, Mathematical biology)
|
We are interested in developing mathematical methodologies to investigate nonlinear dynamical systems. The systems of particular interest are some mathematical models about biological processes or phenomena, including the ones on cell differentiation, somitogenesis, gene regulation, neuronal systems, and competitive species under dispersal. Mathematical analysis on the collective behaviors of these coupled cells or coupled systems enhances the understanding of these models. The other research interest is mathematical theory in neural networks. |
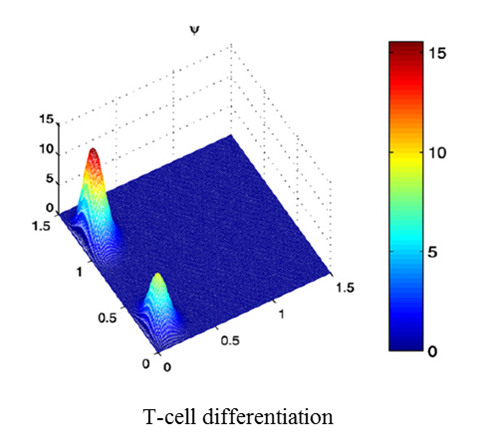 |
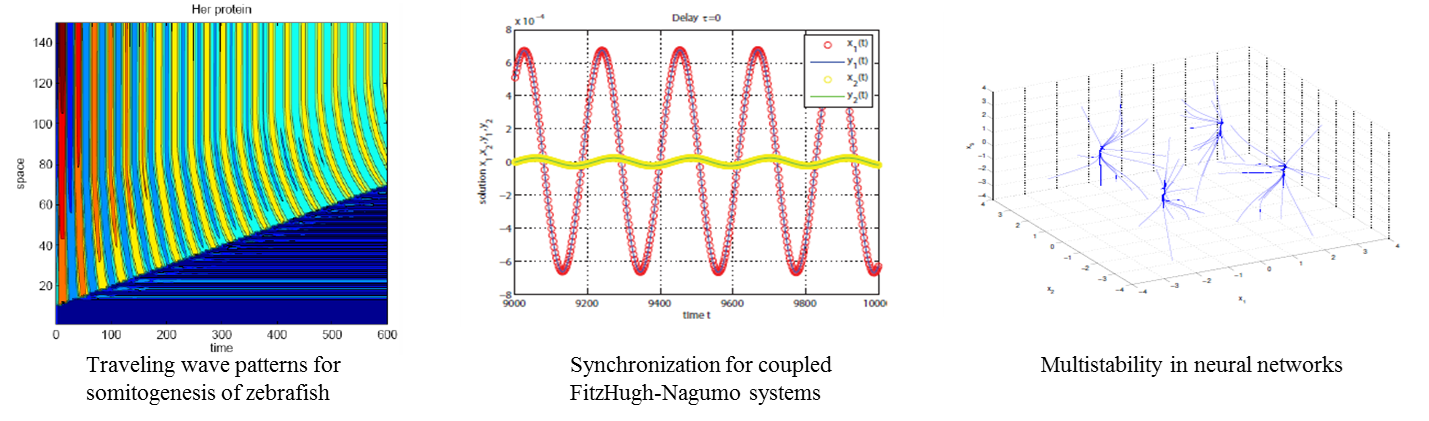 |
Professor Juang, Jong (Coupled Systems, Synchronization, Neural Networks, Neuronal Dynamics, Flocking Problems and Traffic Flow Models)
|
Our research interests are centered around the real world problems that can be modeled by coupled networks. Among the problems under considerations are as follows: (i) Coupled chaotic oscillators; Coupled maps lattices. Our group has been studying synchronization phenomena in coupled systems for the last few years. We develop some analytical theorems to ensure the emerge of synchronization. These results can be applied to the realistic design of electronic circuit system and secure communication (Figure 1). (ii) Biological neural networks; Neural pathways: In the last few decades, the study of the neuronal dynamical behaviors has shifted to a network of neurons from a single neuron. Our group focuses on the study of synchronization phenomena in the neural network and probes the distinct neuronal dynamical behaviors under coupled neural networks (Figure 2). (iii) Flocking behavior; Collective animal behavior exhibited by many living beings such as birds, fish, bacteria and insects: Recently, we consider the flocking behaviors of living beings and discuss the mechanism of avoiding collision between them (Figure 3). (iv) Epidemic models; Disease transmission models : We are also interested in considering the impact of the individual contact networks, awareness and vectors on the disease spreading. (v) Microscopic and macroscopic traffic flow models : The traffic flow problem is one of our research interests. We wish to study some well-known traffic models to explain the traffic flow and the occur of traffic jams. In the future, we aim to use our model to predict and control the traffic flow in freeways of Taiwan. |
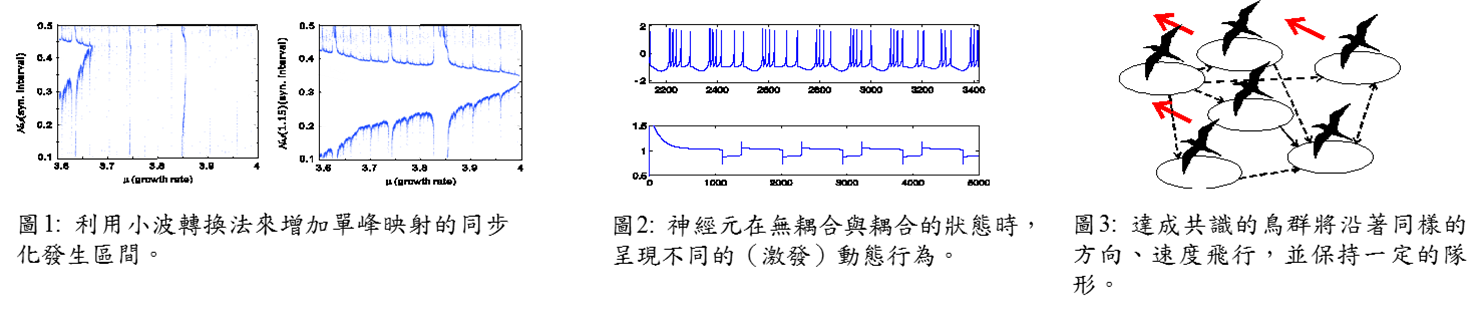 |
Professor Yeh, Li-Ming (Operator Theory, Matrix Analysis, Numerical Ranges)
|
We are interested in transport and diffusion problems in heterogeneous media. These problems arise from contaminant flows in the subsurface, heat transfer in two-phase media, stress in composite materials, etc. Our attention is mostly on the mathematical modeling, convergence analysis, and numerical computations. Consider an elliptic equation in a periodic domain with period size ?. It is known that if ? tends to 0, the solution of the elliptic equation approaches a solution of a simple macroscopic equation. Moreover, a convergence estimate can be derived. Therefore, we would like to ask the same questions for realistic problems. If a mathematical model for a realistic problem is available, is it possible to find a simple macroscopic model so that the solution of the simple model still keeps properties close to those of the original realistic problem when measured on long space-time scales? If yes, can we derive a convergence estimate for the realistic solution? Also is it possible to find a simple way to compute the solution of the original realistic problem? To answer these questions, some basic tools are necessary, for example, knowledge of partial differential equations and ergodic theory, understanding of functional spaces and homogenization methods, and numerical methods. |
Associate Professor Wu, Chin-Tien (Numerical PDE, Finite element, Multigrid, 3d image processing)
|
I am interesting in scientific computing and its applications. In particular, we use finite element method to solve problems from fluid dynamics, elastic mechanics, and geometric optics. In fluid dynamic, we simulate incompressible flow, shallow water and thin film. Robust multigrid methods combined with Krylov iteration are employed to speed up our simulator. In elastic mechanics, we solved the non-linear geometric deformation of thin shell with composite or piezoelectric material. We also apply large diffeomorphic metric map to compute the deformation of 3d images. In geometric optics, we constructed non-image freeforms by solving the Monge-Ampere equation using high order finite element and optimized the design using quantum particle swarm method. Recently, we like to further study on topics including 3d modeling, video tracking and machine learning etc. |
 |
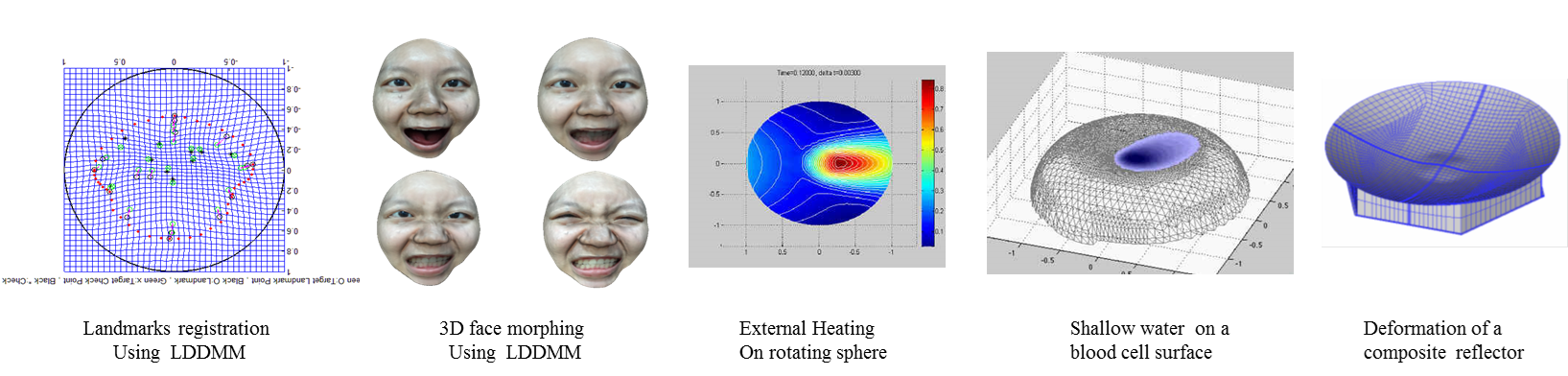 |
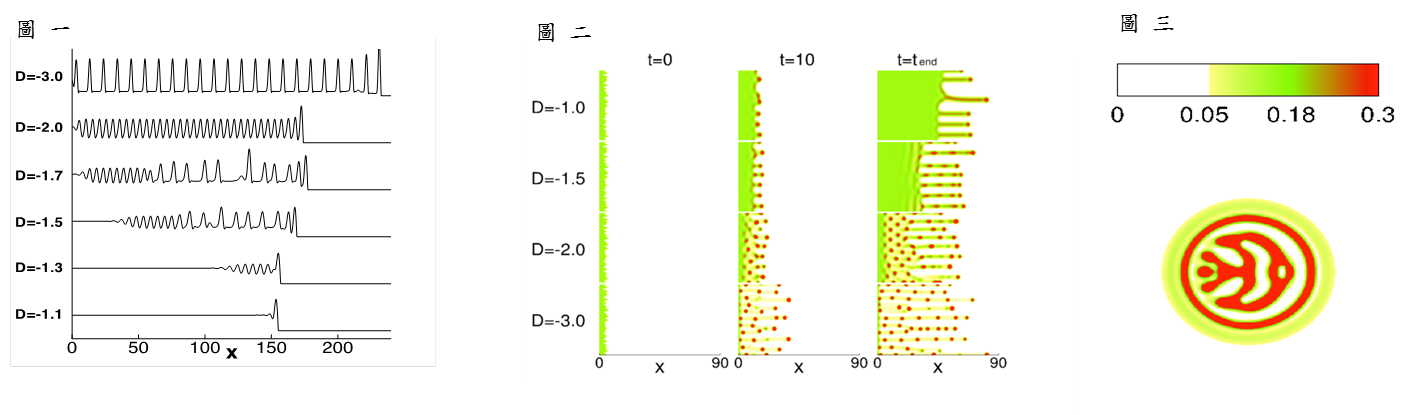
Associate Professor Chang, Shu-Ming (Scientific Computations, Dynamical Systems)
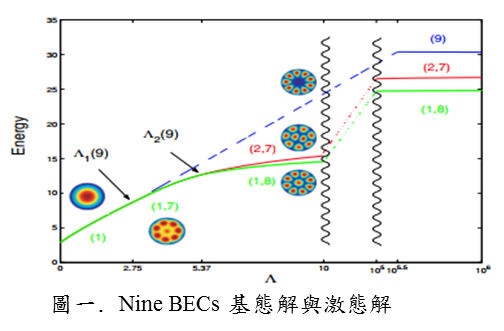
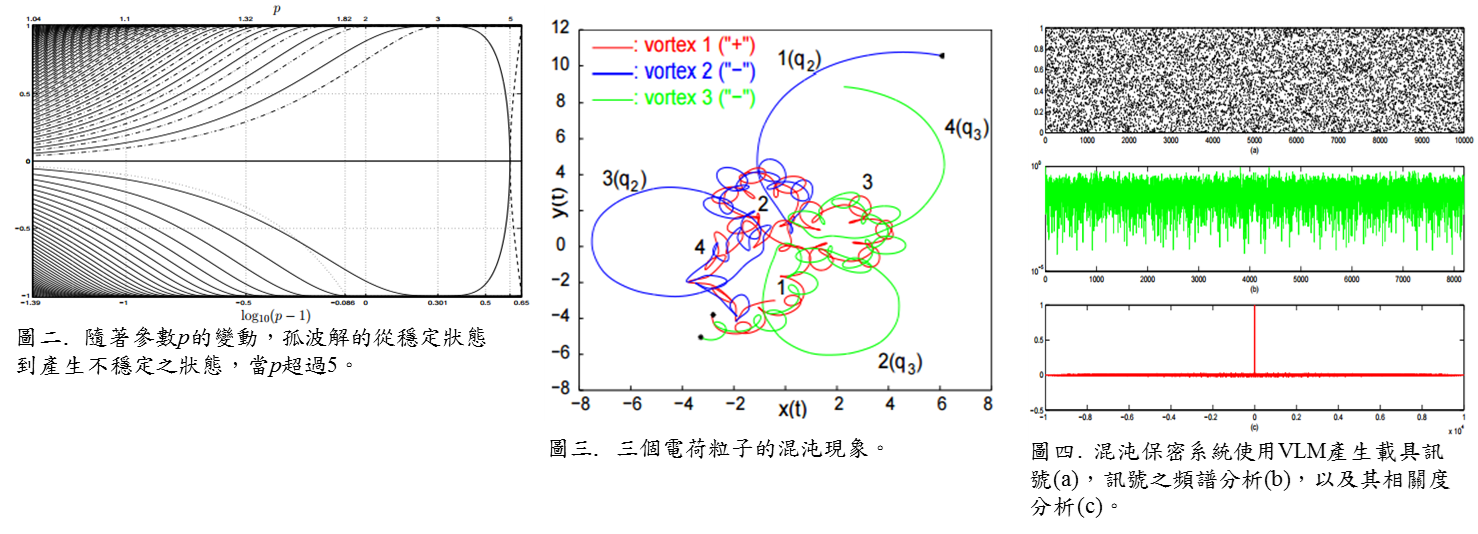
In Scientific Computations, we focus on Numerical Computations of Nonlinear Schrodinger's Equations that there are two researching topics in this field: (1) The Ground State and Excited States for the Bose-Einstein Condensates (BECs) (see Fig. 1), (2) Stability Analysis in the Soliton Waves (see Fig. 2). Then in Dynamical Systems, we focus on Chaotic System and its Applications that there are also two researching topics in this field: (3) Investigation on Chaotic Behavior, (4) Digital Chaotic Generators in Secure Communication (see Fig. 4). |
 |
 |
Assistant Professor Chi-Hin Chan(Analytical, Geometrical, and Topological Properties of Viscous Incompressible Fluid Flows, Partial Differential Equations)
|
The motion of an incompressible Newtonian fluid is described by the incompressible Navier- Stokes equation in the Euclidean space setting. Though the standard derivation of the incompress- ible Navier-Stokes equation based on the Newton’s second law was well-understood already in the 19 century, serious mathematical study of viscous incompressible fluid flows from the view point of Partial Differential Equations only began with the existence theory of Leray-Hopf weak solutions to the incompressible Navier-Stokes equation as established by Leray (1930’s) and Hopf (1950’s). Since then, P.D.E. specialists in this area had devoted great efforts in obtaining the classical smoothness property of Leray-Hopf weak solutions under suitable space-time integrability condi- tions imposed on the weak solutions themselves. However, it is still a long standing open problem to decide whether the breakdown of classical smoothness of Leray-Hopf weak solutions could occur. My research focuses on the study of analytical, geometrical, and topological properties of viscous fluid flows taking place in a curved space setting. In the past few years, I and professor Magdalena Czubak made a simple yet striking observation about the non-uniqueness phenomena of finite energy viscous fluid flows on a negatively curved surface of constant sectional curvature. and subsequentally established the proper framework of weak solutions which restores uniqueness in the same setting. In the near future, we will try to find a deeper connection between mathematical properties of fluid flows taking place in a curved space setting and those of fluid flows taking place in the standard flat space setting. |
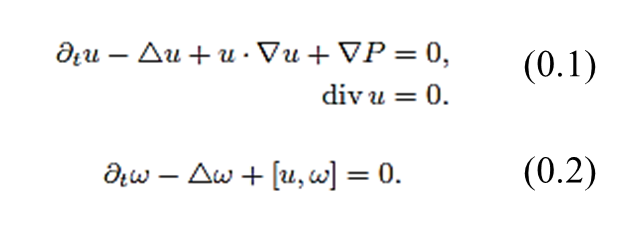 |
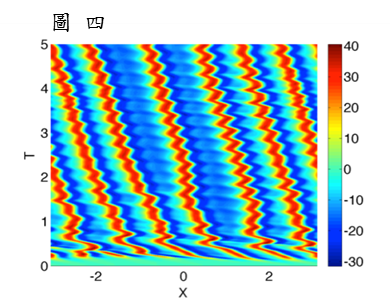
Assistant Professor Te-Sheng Lin (Mathematical modeling, Scientific computing, Fluid mechanics, Asymptotic analysis)
|
The focus of my research is concerned with the development of analytical and computational tools for the problems that arises in fluid dynamics, currently in thin liquid films, and further to communicate with scientists from other disciplines to solve engineering problems in practice. My current research topics includes (1) Fingering instabilities in Newtonian films; (2) Modeling and analysis of nematic droplets and films; (3) Coherent structures in non-local dispersive active-dissipative systems; (4) Pulse interaction and bound state formation in electrified falling films. For example, Figures. 1 and 2 present 2D and 3D numerical simulations of fingering instabilities arising in falling liquid films, respectively. Figure 3 presents the pattern formation on a thin film of nematic liquid crystal. Figure 4 shows the simulation that represents a liquid film sheared by a turbulent gas. |
 |
 |
Assistant Professor Ming-Cheng Shiue (Numerical Analysis, Scientific Computing, Geophysical Fluid Dynamics)
|
Currently, my research interests focus on analysis and computation of the Partial Differential Equations (PDEs) arising from geophysical fluid dynamics. For example, equations related to weather prediction and oceanography are the inviscid Primitive Equations (PEs) and the Shallow Water Equations (SWEs). In Figure 1, the basic level of physical complexity in geophysical fluid dynamics is presented. The Navier-Stokes equations govern the motion of the fluid. In the ocean or atmosphere, due to the thin layer structure (the ratio of the vertical scale of the domain to the horizontal scale is relatively small), Navier-Stokes equation can be simplified in the form of Primitive equations. Shallow water equations are derived from the first mode of the Primitive equations. |
 |
|
The following issues are focused: For more details, please see my homepage (Figure 2). |
Assistant Professor Ming-Cheng Shiue (Numerical Analysis, Scientific Computing, Geophysical Fluid Dynamics)
|
A general principle in many areas of mathematics and science is that the dynamics of a system tend to evolve in a direction which reduces the available energy. This is the least action principle, which postulates the possibility of defining an energy - a functional whose input is taken from a set of possible states - and supposing that the output or “action” of that state prefers local minima. From this perspective, the calculus of variations is very important, since it is precisely the study of the extrema of functionals. Our research focuses on the regularity of minimizers and how the qualitative properties depend on the differential order of the energy. Here we utilize an object whose study in the literature is surprisingly quite sparse – Riesz fractional gradients – and early research suggests that although there are significant differences in the properties of energies of integer differential order, there is no difference in the regularity or qualitative properties. Thus far we have obtained several new existence and convergence results for the Partial Differential Equations we consider, as well as new inequalities that provide a nice complement to more classical results. Future research will look to new regularity results for non-linear problems as well as the application to physical problems modeled by these energies. |
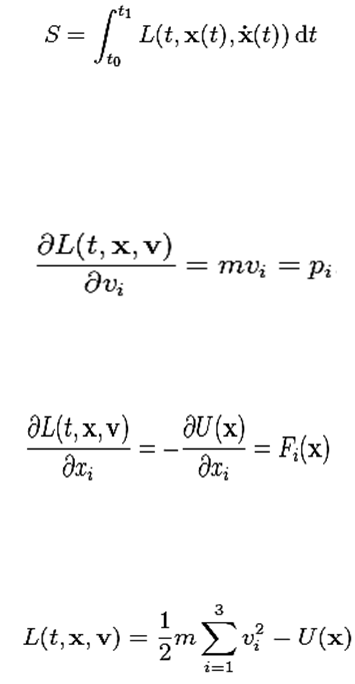 |
Assistant Professor Yu, Chi-Jer (Scientific Computation, Differential Equations)
TopAnnual Courses Related to Scientific Computation:
- Ordinary Differential Equations (Sophomore)
- Numerical Analysis (Junior, Graduate)
- Scientific Computation (Junior, Senior, Graduate)
- Mathematics of Semiconductor and Software Engineering (Junior, Senior, Graduate)
- Matrix Computation (Junior, Senior, Graduate)
- Numerical Partial Differential Equations (Junior, Senior, Graduate)
- Real Analysis (Junior, Senior, Graduate)
- Functional Analysis (Graduate)
- Applied Functional Analysis (Graduate)
- Partial Differential Equations (Sophomore, Graduate)
- Applied Mathematics methods (Graduate)
- Finite Element methods (Graduate)
Top
Graduates and Employment:
There are a total of 60 M.S. and Ph.D. graduates with a wide range of careers such as teachers in colleges, technical schools, or high schools, and researchers in research centers. Moreover, quite a number of our M.S. and Ph.D. graduates are software engineers in industries. Top
Top