Research Fields: Financial Engineering and Probability

We study the problem of disorder chaos in the spherical mean-_field model. It concerns the behavior of the overlap between two independently sampled spin configurations from two Gibbs measures with the same external parameters. The prediction states that if the disorders in the Hamiltonians are slightly decoupled, then the overlap will be concentrated near a constant value. Following Guerraбеs replica symmetry breaking scheme, we establish this at the levels of the free energy and the Gibbs measure.

The Markov chain Monte Carlo (briefly, MCMC) method is a well-designed algorithm in sampling probability measures on discrete sets. Along with the Metropolis-Hasting algorithm, one may implement the MCMC method only with the local information of the targeted distributions, say the relative ratio, but without the information of the normalizing constant. When the MCMC method is simulated, it is important to select a (deterministic or random) time, say T, to stop the algorithm for sampling. Theoretically, the stopping time T can be the mixing time or the coupling time but none of them is easy to achieve.

The cutoff phenomenon is a phase-transit phenomenon in the evolution of Markov chains. This concept was introduced by Aldous and Diaconis in early 1980s in order to catch up the observation that the distribution of Markov chain is far from its stationarity before a time S and, after a relatively short period compared with S, the distribution turns out to be almost the limiting distribution. When a cutoff exists in a MCMC algorithm, the time S can be a good candidate for the stopping time of algorithm.

The MCMC method arises in many disciplines including the statistic physics, computer science, molecular biology, mathematical finance and more. From the viewpoint of interdisciplinary research, the underlying machinery can be very complicated, e.g. random walks on disordered random media and Markov processes on compact Riemannian manifolds, and a quick formula on the stopping time T and the cutoff time S will be very challenging but highly expected.

The following are some future perspectives we are interested in.
(1) Spectral analysis of graph connection Laplacian
(2) Random walks on random media
(3) Inhomogeneous Markov chains

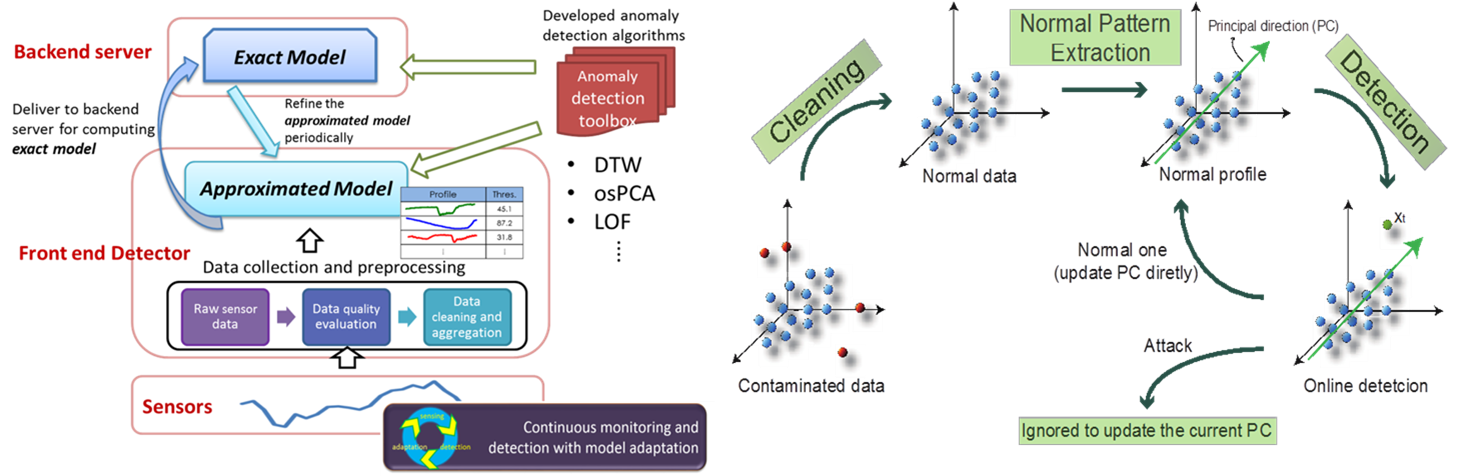
My research is primarily rooted in optimization theory and spans a range of areas including machine learning, data mining, big data, numerical optimization and operations research. During the last decade, I have developed many learning algorithms in supervised learning, semi-supervised learning and unsupervised learning as well as linear/ nonlinear dimension reduction. My recent major research is applying machine learning to information security problems such as network intrusion detection, anomaly detection, malicious URLs detection and legitimate user identification. Currently, I focus on online learning algorithms for dealing with large scale datasets based on stochastic optimization. I am interested in exploring numerical techniques such as accelerated stochastic gradient, Hessian inverse approximation and the second order information. The compressed sensing, dictionary learning and sparse coding are other major research interests. I believe that all these research topics play extremely important roles in Big Data as well as Internet of Things (IoT) data analytics.