Research Fields: Discrete Mathematics and Optimization

Quick links

General Introduction to Combinatorics
Research Interests

I. General Introduction to Combinatorics

We will break the introduction into 5 sections：

What is Combinatorics ?
Combinatorics is equivalently known as Discrete Mathematics. From the very beginning of the study of mathematics, arithmetic and geometry represent the origins of discreteness and continuity. The two concepts intertwined into the wonderful world of mathematics. But since the invention, called the calculus, of Newton, analysis had been at the center of attention for almost three hundred years. Although the origins of various topics of modern day discrete mathematics can be traced back to number theory, algebra, probability and elementary geometry, it still has not reached a state of significance and maturity. It is even limited to the form of recreational puzzles with ocean deep potential waiting to be explored.

Since the beginning of this century however, methods and tools of discrete mathematics have started to gain momentum and been widely applied and developed in the scientific community. Gradually, discrete mathematics became a new focus and was regarded a discipline of its own. Some related research fields have started to gather under the umbrella of discrete mathematics (combinatorics). Especially after the 30's, the science of computation has gained revolutionary development both in theory and practicality. Digital computer, a powerful data processing machine, has propelled human civilization to a whole new dimension. It not only facilitates daily lives but also deeply influences our mindset and advancement of human knowledge. Computer operates discretely; it reformulates classical continuous mathematical models into discrete ones which have become significant discrete problems of their own. All of this further establishes the significance of discrete mathematics. Moreover, the enormous processing power of the computer on finite quantities and structures has opened up a whole new frontier and brought in new meanings and challenges.
What does Combinatorics include ?
Combinatorics is a general term which includes a number of areas, a few of the major areas are :
1. Classical counting problems include combinatorial problems on finite collection of sets;
2. The construction of combinatorial structures based on Algebra and Topological methods;
3. Design Theory based on Group Theory and Finite Geometry;
4. Graph Theory, Network, and Theory of Hypergraphs;
5. Optimization, Operational Research, and Game Theory;
6. Coding Theory and Cryptography;
7. Matroid and generalized Greedoid Theory;
8. Discrete and Arithmetic Geometry;
9. Design and analysis of the principle of Algorithm.
Top
What are the applications of Combinatorics ?
The largest application is in Computer Science in which Combinatorics is a required course. All digitized products like laser disc, compact disc, mobile phones, satellite communication etc. depend on error correcting code to increase their reliability; ATM card, credit card depend on cryptography; without which daily life will be halted. Furthermore, genetic sequencing problem, option analysis, the stability and food chain, experiment design, are some of the common applications of Combinatorics. Predictably, the demand for combinatorics by non mathematics disciplines will substantially increase. Some even advocate that combinatorics should replace calculus as the fundamental mathematics course for freshmen.
The Department and Combinatorics :
Our department has the highest number of faculties, among Taiwan universities, in combinatorics covering all major areas of combinatorial research; among the faculty, Honorary Professor Frank Hwang is a world renowned expert in combinatorics.
1. Professor Frank Hwang(Specialty: Combinatorial Optimization, Operational Research, Network Design)
2. Professor Fu, Hung-Lin(Specialty: Graph Theory, Combinatorial Design)
3. Professor Huang, Ta-Yuan(Specialty: Algebraic Combinatorics, Finite Geometry)
4. Professor Weng, Chih-Wen(Specialty: Algebraic Combinatorics, Matrix Theory)
5. Professor Chen, Chiu-Yuan(Specialty: Algorithm, Graph Theory, Discrete Mathematics)
6. Assistant Professor Michael Fuchs(Specialty: Metric Number Theory, Analysis of Algorithms)
Top
All courses offered in previous years are listed below. Graduate level courses are generally offered to graduate students once in two years to allow a wider exposure in their two-year M.S. program :
1. Discrete Mathematics I (Undergraduate Required Course)
2. Discrete Mathematics II (Undergraduate)
3. Coding Theory (Undergraduate & Graduate)
4. Combinatorial Coding (Graduate)
5. Cryptography (Undergraduate & Graduate)
6. Topics in Discrete Mathematics (Graduate Required Course)
7. Graph Theory I & II (Graduate Required Courses)
8. Design Theory (Graduate)
9. Algebraic Combinatorics (Graduate)
10. Algebraic Graph Theory (Graduate)
11. Probability Graph Theory (Graduate)
12. Algorithm (Undergraduate & Graduate)
13. Graph Theory Algorithm (Undergraduate & Graduate)
14. Analysis of Algorithms (Graduate)
15. Combinatorial Optimization (Undergraduate & Graduate)
16. Connected Networks (Graduate)
17. Group Testing Theory (Graduate)
18. Optimal Partition (Graduate)
Combinatorics division is one of the two graduate divisions of our department. The annual intake has increased over the year from five to the current thirteen. PhD degree intake is flexible. Our department has graduated over thirty highly acclaimed PhDs establishing their careers in major local universities.
Top
Connection to Other Departments of nycu :
Combinatorics related courses offered by other departments in nycu are as follows:
1. Discrete Mathematics
  (Department of Electrical and Control Engineering-Undergraduate, Department of Computer Science and Information Engineering-Undergraduate, Department of Computer Science-Undergraduate)
2. Combinatorics
  (Department of Computer Science-Undergraduate)
3. Operational Research
  (Institute of Information Management, Department of Management Science-Undergraduate, Department of Transportation Technology and Management-Undergraduate, Department of Industrial Engineering and Management-Undergraduate)
4. Linear Programming
  (Department of Computer Science and Information Engineering-Undergraduate)
5. Graph Theory
  (Department of Computer Science and Information Engineering-Graduate, Department of Computer Science-Graduate/Undergraduate)
6. Connected Network
  (Department of Computer Science and Information Engineering-Graduate, Department of Computer Science-Graduate)
7. Cryptographic Methods
  (Department of Computer Science and Information Engineering-Graduate, Department of Computer Science-Graduate)
8. Introduction to Cryptography
  (Department of Computer Science and Information Engineering-Graduate, Department of Computer Science-Graduate)
9. Advanced Cryptography
  (Department of Computer Science-Graduate)
10. Channel Coding
  (Department of Electronics Engineering-Graduate/Undergraduate)
11. Coding Theory
  (Department of Communication Engineering-Graduate/Undergraduate)
12. Information Theory
  (Department of Communication Engineering-Graduate)
13. Algorithm
  (Department of Computer Science and Information Engineering-Graduate/Undergraduate, Department of Computer Science-Graduate)
14. Introduction to Algorithm
  (Department of Computer Science and Information Engineering-Undergraduate)
15. Algorithm and Structure
  (Department of Computer Science and Information Engineering-Graduate/Undergraduate)
16. Distributed Algorithm
  (Department of Computer Science and Information Engineering-Graduate, Department of Computer Science-Graduate)
17. Genetic Algorithm
  (Department of Compute Science-Graduate)

Top

II. Research Interests:

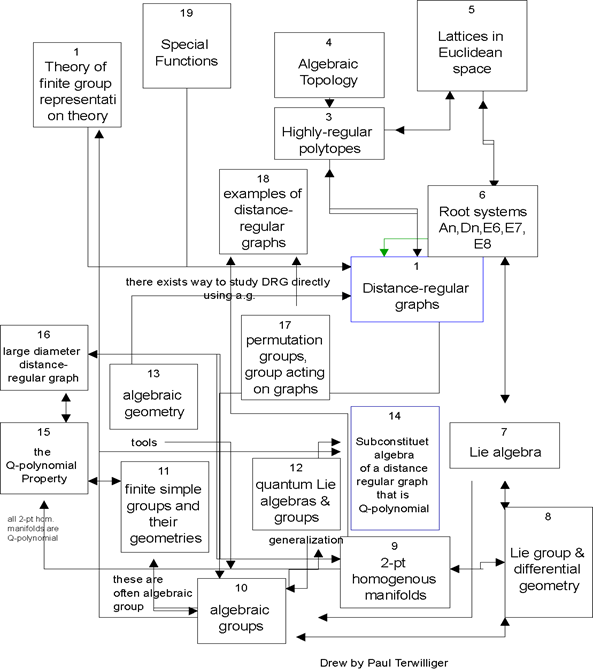
Professor Tayuan Huang(Algebraic Combinatorics, Finite Geometry)

The structure of P-polynomial association schemes is a class of combinatorial structures originated from experimental designs in statistics, which have the properties of high regularity and symmetry. It has close relationship with groups, orthogonal polynomials, lattices, metric spaces, codes and combinatorial designs nowadays.

These structures also appear in algebraic combinatorics as distance regular graphs. My research interests are mainly those high regularity and symmetric property associated with distance regular graphs, including

finite geometry – geometric constraints
intersection arrays - combinatorial constraints
spectra – linear algebraic constraints
Bose- mesner algebras – algebra constraints

The notion of symmetric spin models was first introduced by Jones, and Kauffman around 1984-1989 for dealing with polynomial invariants of knots, and they were soon generalized to two-weight, four-weight spin models respectively. Possible explicit relationship between four-weight spin models and Bose-Mesner algebras are also interesting to us.

The current focus of interests is the possible roles played by the structure of distance regular graphs and association schemes in pooling designs of various models.

Top

Professor Hung-Lin Fu (Combinatorial Design, Graph Theory and their Applications)

My recent research includes the following topics:

Study Group Testing with various models which are applicable in computational molecular biology.
Construct conflict-avoiding codes by way of special sequences which we constructed and weighted matchings with suitable models.
Use the new idea we developed called core cluster to find the optimal average information ratio of perfect secret-sharing schemes for the access structures based on graphs.
Obtain good adaptive algorithms in finding hidden graphs and hypergraphs, this result is important in DNA sequencing.
Construct codes with the identifiable parent property for multimedia fingerprinting.
Find the global packing number of special networks which are useful in communication design.
Find the vertex feedback number of graphs which are of good application in preventing network deadlocks.

Top

Professor Chiuyuan Chen(Graph Theory, Computer Algorithms, Interconnection Networks and Wireless Networks)

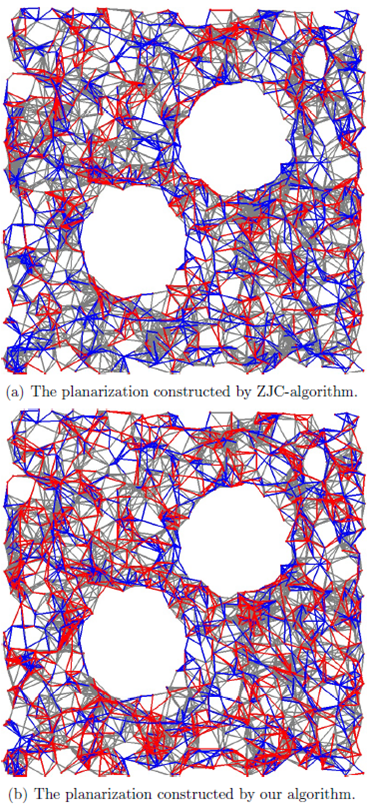
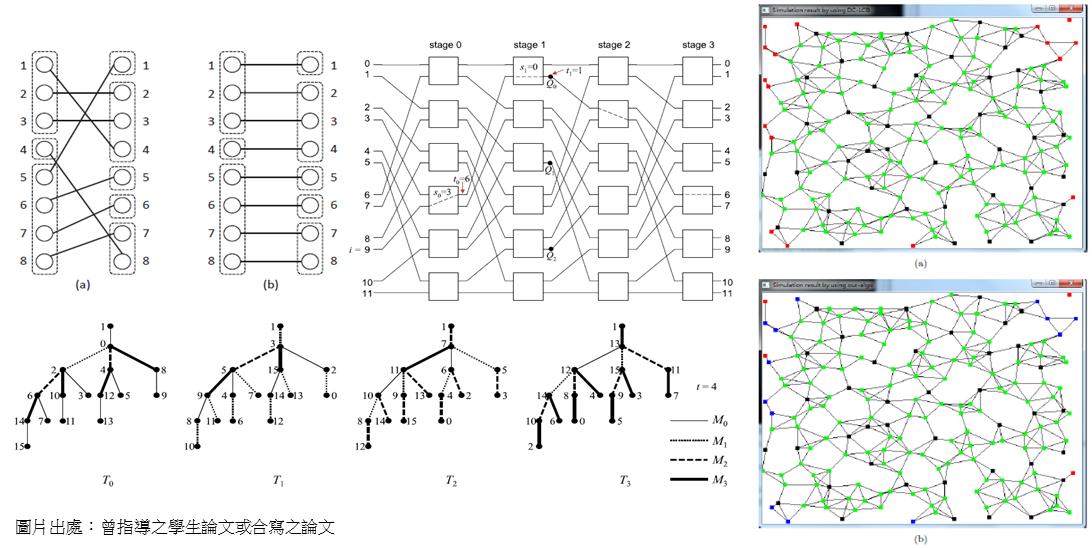
Recent Research Projects

(1)The application of graph theory to the localization and routing problems in wireless sensor networks
(2)Distance-two coloring for the adjacency graphs of wireless sensor networks
(3)The applications of graph theory to wireless sensor networks (data aggregation and localization)

Top

Professor Chih-Wen Weng (Distance-Regular Graphs, Group Testings, Presentation and Representation Theory, Combinatorial Matrix Theory, Graph Theory)

Yu-pei Huang, Yeh-jong Pan and Chih-wen Weng, Nonexistence of a Class of Distance-Regular Graphs, the electronic journal of combinatorics, Volume 22, Issue 2 (2015), #P2.37
(Show the nonexistence of a class of DRG)

Jun Guo, Kaishun Wang, Chih-wen Weng, Pooling semilattices and non-adaptive pooling designs, Discrete Mathematics 320(2014), 64-72
(Construct pooling designs from semilattices)

Chia-an Liu, Chih-wen Weng, Spectral radius of bipartite graphs, Linear Algebra and its Applications, 474(2015), 30–43
(Provide a sharp upper bound of bipartite graphs)

Yen-Jen Cheng, Feng-lei Fan, Chih-wen Weng, An extending result on spectral radius of bipartite graphs, arXiv:1509.07586
(Provide a spectral characterization of twin primes)

http://jupiter.math.nycu.edu.tw/~weng/weng.htm

Top

Research Summary in Combinatorics Group of NYTU

Distance-Regular Graphs: The classification of distance-regular graphs by their spectrums, intersection numbers or other algebraic properties and combinatorial properties. Study other algebraic or combinatorial subjects related to distance-regular graphs, e.g. bent functions, spin models, bidiagonal pairs, quantum algebra.
Combinatorial Designs related to Group Testing: The construction of pooling designs via graph decompositions and poset structures from finite geometries. The relations between different pooling designs, e.g. the relation between d-separable and d-disjunct matrices.
Networks: The construction of networks by combinatorial method and algebraic method. The network properties related to general graph theory and number theory, e.g. graph coloring, graph connectivity, Euclidean division algorithm. The network properties related to geometrical properties, e.g. L-shape in Euclidean plane. The behavior of a particular network.
General Graph Theory: The study of vertex coloring, edge coloring, graph labeling, planar graphs, Hamiltonian paths or cycles, and other related graph properties.